What Effect Does The Initial Temperature Of The Water Have On The Change In Temperature
Heat and Heat Transfer Methods
101 Temperature Alter and Oestrus Capacity
Learning Objectives
- Observe heat transfer and change in temperature and mass.
- Calculate final temperature after heat transfer between 2 objects.
One of the major effects of heat transfer is temperature change: heating increases the temperature while cooling decreases it. Nosotros assume that there is no phase change and that no work is washed on or by the system. Experiments show that the transferred heat depends on three factors—the change in temperature, the mass of the system, and the substance and stage of the substance.
The dependence on temperature change and mass are easily understood. Owing to the fact that the (average) kinetic energy of an atom or molecule is proportional to the absolute temperature, the internal free energy of a arrangement is proportional to the absolute temperature and the number of atoms or molecules. Owing to the fact that the transferred estrus is equal to the change in the internal energy, the estrus is proportional to the mass of the substance and the temperature change. The transferred heat also depends on the substance and then that, for example, the heat necessary to raise the temperature is less for booze than for water. For the same substance, the transferred heat likewise depends on the phase (gas, liquid, or solid).
Values of specific heat must generally exist looked up in tables, considering at that place is no simple way to calculate them. In full general, the specific rut also depends on the temperature. (Figure) lists representative values of specific heat for diverse substances. Except for gases, the temperature and volume dependence of the specific estrus of nearly substances is weak. We come across from this table that the specific rut of water is five times that of glass and ten times that of iron, which ways that it takes 5 times equally much heat to enhance the temperature of h2o the aforementioned corporeality as for glass and ten times as much estrus to raise the temperature of water as for atomic number 26. In fact, water has one of the largest specific heats of any material, which is important for sustaining life on Earth.
Calculating the Required Rut: Heating Water in an Aluminum Pan
A 0.500 kg aluminum pan on a stove is used to heat 0.250 liters of h2o from ![]() to
to ![]() . (a) How much estrus is required? What percentage of the heat is used to raise the temperature of (b) the pan and (c) the water?
. (a) How much estrus is required? What percentage of the heat is used to raise the temperature of (b) the pan and (c) the water?
Strategy
The pan and the water are always at the same temperature. When yous put the pan on the stove, the temperature of the water and the pan is increased by the aforementioned corporeality. We use the equation for the heat transfer for the given temperature change and mass of h2o and aluminum. The specific heat values for water and aluminum are given in (Effigy).
Solution
Because water is in thermal contact with the aluminum, the pan and the water are at the same temperature.
- Calculate the temperature difference:
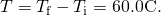
- Calculate the mass of water. Considering the density of water is
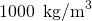 , one liter of h2o has a mass of 1 kg, and the mass of 0.250 liters of water is
, one liter of h2o has a mass of 1 kg, and the mass of 0.250 liters of water is 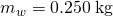 .
. - Summate the oestrus transferred to the water. Utilise the specific rut of water in (Figure):
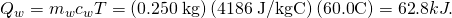
- Calculate the heat transferred to the aluminum. Use the specific estrus for aluminum in (Effigy):
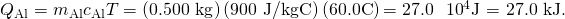
- Compare the percentage of heat going into the pan versus that going into the water. First, observe the total transferred heat:
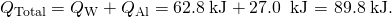
Thus, the amount of heat going into heating the pan is
![]()
and the corporeality going into heating the h2o is
![]()
Discussion
In this example, the heat transferred to the container is a meaning fraction of the total transferred heat. Although the mass of the pan is twice that of the h2o, the specific estrus of water is over four times greater than that of aluminum. Therefore, it takes a bit more than twice the estrus to achieve the given temperature change for the water as compared to the aluminum pan.
The smoking brakes on this truck are a visible evidence of the mechanical equivalent of oestrus.

Calculating the Temperature Increase from the Work Done on a Substance: Truck Brakes Overheat on Downhill Runs
Truck brakes used to control speed on a downhill run practise work, converting gravitational potential energy into increased internal energy (higher temperature) of the restriction fabric. This conversion prevents the gravitational potential energy from beingness converted into kinetic energy of the truck. The problem is that the mass of the truck is large compared with that of the brake material arresting the energy, and the temperature increase may occur too fast for sufficient rut to transfer from the brakes to the environment.
Calculate the temperature increment of 100 kg of brake material with an boilerplate specific heat of ![]() if the cloth retains 10% of the free energy from a ten,000-kg truck descending 75.0 m (in vertical displacement) at a constant speed.
if the cloth retains 10% of the free energy from a ten,000-kg truck descending 75.0 m (in vertical displacement) at a constant speed.
Strategy
If the brakes are not applied, gravitational potential free energy is converted into kinetic energy. When brakes are applied, gravitational potential energy is converted into internal energy of the brake material. We first calculate the gravitational potential energy ![]() that the entire truck loses in its descent and then detect the temperature increment produced in the brake textile alone.
that the entire truck loses in its descent and then detect the temperature increment produced in the brake textile alone.
Solution
- Calculate the change in gravitational potential energy as the truck goes downhill
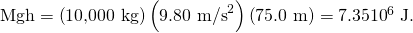
- Calculate the temperature from the heat transferred using
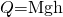 and
and 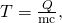
where
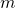 is the mass of the brake material. Insert the values
is the mass of the brake material. Insert the values 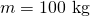 and
and 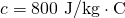 to find
to find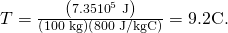
Discussion
This aforementioned idea underlies the contempo hybrid engineering of cars, where mechanical energy (gravitational potential energy) is converted by the brakes into electric energy (battery).
| Substances | Specific heat (c) | |
|---|---|---|
| Solids | J/kg⋅ºC | kcal/kg⋅ºC2 |
| Aluminum | 900 | 0.215 |
| Asbestos | 800 | 0.19 |
| Concrete, granite (average) | 840 | 0.20 |
| Copper | 387 | 0.0924 |
| Drinking glass | 840 | 0.xx |
| Gold | 129 | 0.0308 |
| Human body (average at 37 °C) | 3500 | 0.83 |
| Water ice (average, -fifty°C to 0°C) | 2090 | 0.l |
| Iron, steel | 452 | 0.108 |
| Atomic number 82 | 128 | 0.0305 |
| Silverish | 235 | 0.0562 |
| Wood | 1700 | 0.iv |
| Liquids | ||
| Benzene | 1740 | 0.415 |
| Ethanol | 2450 | 0.586 |
| Glycerin | 2410 | 0.576 |
| Mercury | 139 | 0.0333 |
| H2o (15.0 °C) | 4186 | one.000 |
| Gases 3 | ||
| Air (dry) | 721 (1015) | 0.172 (0.242) |
| Ammonia | 1670 (2190) | 0.399 (0.523) |
| Carbon dioxide | 638 (833) | 0.152 (0.199) |
| Nitrogen | 739 (1040) | 0.177 (0.248) |
| Oxygen | 651 (913) | 0.156 (0.218) |
| Steam (100°C) | 1520 (2020) | 0.363 (0.482) |
Note that (Effigy) is an analogy of the mechanical equivalent of rut. Alternatively, the temperature increment could be produced by a blow torch instead of mechanically.
Calculating the Concluding Temperature When Estrus Is Transferred Between Ii Bodies: Pouring Cold Water in a Hot Pan
Suppose y'all pour 0.250 kg of ![]() h2o (most a cup) into a 0.500-kg aluminum pan off the stove with a temperature of
h2o (most a cup) into a 0.500-kg aluminum pan off the stove with a temperature of ![]() . Assume that the pan is placed on an insulated pad and that a negligible amount of water boils off. What is the temperature when the water and pan reach thermal equilibrium a brusque time later on?
. Assume that the pan is placed on an insulated pad and that a negligible amount of water boils off. What is the temperature when the water and pan reach thermal equilibrium a brusque time later on?
Strategy
The pan is placed on an insulated pad so that little estrus transfer occurs with the surround. Originally the pan and water are not in thermal equilibrium: the pan is at a higher temperature than the water. Estrus transfer then restores thermal equilibrium once the h2o and pan are in contact. Because oestrus transfer between the pan and water takes place rapidly, the mass of evaporated h2o is negligible and the magnitude of the estrus lost by the pan is equal to the heat gained past the water. The commutation of heat stops once a thermal equilibrium between the pan and the water is achieved. The heat exchange tin be written equally ![]() .
.
Solution
- Use the equation for oestrus transfer
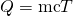 to limited the heat lost past the aluminum pan in terms of the mass of the pan, the specific heat of aluminum, the initial temperature of the pan, and the concluding temperature:
to limited the heat lost past the aluminum pan in terms of the mass of the pan, the specific heat of aluminum, the initial temperature of the pan, and the concluding temperature: 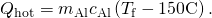
- Express the heat gained by the water in terms of the mass of the water, the specific oestrus of h2o, the initial temperature of the h2o and the final temperature:
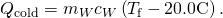
- Note that
 and
and 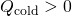 and that they must sum to nix because the rut lost by the hot pan must be the same as the heat gained by the cold water:
and that they must sum to nix because the rut lost by the hot pan must be the same as the heat gained by the cold water: 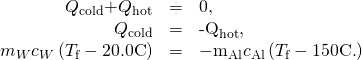
- Bring all terms involving
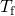 on the left hand side and all other terms on the right mitt side. Solve for
on the left hand side and all other terms on the right mitt side. Solve for 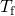 ,
, 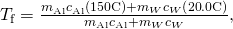
and insert the numerical values:
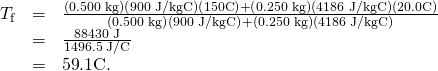
Discussion
This is a typical calorimetry trouble—two bodies at dissimilar temperatures are brought in contact with each other and commutation estrus until a common temperature is reached. Why is the final temperature so much closer to ![]() than
than ![]() ? The reason is that h2o has a greater specific heat than most common substances and thus undergoes a small temperature change for a given estrus transfer. A large torso of h2o, such as a lake, requires a large amount of heat to increase its temperature appreciably. This explains why the temperature of a lake stays relatively constant during a day even when the temperature change of the air is large. However, the water temperature does change over longer times (eastward.thousand., summertime to wintertime).
? The reason is that h2o has a greater specific heat than most common substances and thus undergoes a small temperature change for a given estrus transfer. A large torso of h2o, such as a lake, requires a large amount of heat to increase its temperature appreciably. This explains why the temperature of a lake stays relatively constant during a day even when the temperature change of the air is large. However, the water temperature does change over longer times (eastward.thousand., summertime to wintertime).
Take-Domicile Experiment: Temperature Change of Land and H2o
What heats faster, land or h2o?
To study differences in heat capacity:
- Identify equal masses of dry sand (or soil) and water at the same temperature into 2 small-scale jars. (The average density of soil or sand is about one.6 times that of water, so you tin accomplish approximately equal masses past using
*** QuickLaTeX cannot compile formula: \text{50%} *** Fault bulletin: File ended while scanning use of \text@. Emergency finish.more water by volume.)
- Heat both (using an oven or a heat lamp) for the same amount of time.
- Tape the final temperature of the two masses.
- Now bring both jars to the same temperature by heating for a longer period of time.
- Remove the jars from the heat source and measure their temperature every 5 minutes for about xxx minutes.
Which sample cools off the fastest? This activeness replicates the phenomena responsible for country breezes and sea breezes.
Check Your Agreement
If 25 kJ is necessary to raise the temperature of a cake from ![]() to
to ![]() , how much rut is necessary to heat the block from
, how much rut is necessary to heat the block from ![]() to
to ![]() ?
?
The oestrus transfer depends only on the temperature difference. Since the temperature differences are the same in both cases, the aforementioned 25 kJ is necessary in the 2nd case.
Summary
Conceptual Questions
What three factors affect the heat transfer that is necessary to change an object's temperature?
Bug & Exercises
On a hot day, the temperature of an 80,000-L pond pool increases by ![]() . What is the internet heat transfer during this heating? Ignore any complications, such equally loss of water by evaporation.
. What is the internet heat transfer during this heating? Ignore any complications, such equally loss of water by evaporation.
![]()
Evidence that ![]() .
.
To sterilize a fifty.0-g glass babe bottle, nosotros must raise its temperature from ![]() to
to ![]() . How much heat transfer is required?
. How much heat transfer is required?
![]()
The aforementioned heat transfer into identical masses of different substances produces different temperature changes. Calculate the final temperature when 1.00 kcal of heat transfers into 1.00 kg of the post-obit, originally at ![]() : (a) water; (b) concrete; (c) steel; and (d) mercury.
: (a) water; (b) concrete; (c) steel; and (d) mercury.
Rubbing your hands together warms them past converting piece of work into thermal energy. If a woman rubs her easily dorsum and forth for a total of 20 rubs, at a distance of seven.50 cm per rub, and with an boilerplate frictional strength of forty.0 N, what is the temperature increase? The mass of tissues warmed is just 0.100 kg, mostly in the palms and fingers.
![]()
A 0.250-kg block of a pure material is heated from ![]() to
to ![]() by the addition of 4.35 kJ of energy. Calculate its specific heat and identify the substance of which it is virtually likely composed.
by the addition of 4.35 kJ of energy. Calculate its specific heat and identify the substance of which it is virtually likely composed.
Suppose identical amounts of rut transfer into different masses of copper and h2o, causing identical changes in temperature. What is the ratio of the mass of copper to h2o?
x.8
(a) The number of kilocalories in food is adamant past calorimetry techniques in which the nutrient is burned and the amount of heat transfer is measured. How many kilocalories per gram are in that location in a v.00-g peanut if the energy from burning it is transferred to 0.500 kg of h2o held in a 0.100-kg aluminum cup, causing a ![]() temperature increase? (b) Compare your respond to labeling information found on a package of peanuts and comment on whether the values are consequent.
temperature increase? (b) Compare your respond to labeling information found on a package of peanuts and comment on whether the values are consequent.
Following vigorous exercise, the body temperature of an fourscore.0-kg person is ![]() . At what rate in watts must the person transfer thermal free energy to reduce the the body temperature to
. At what rate in watts must the person transfer thermal free energy to reduce the the body temperature to ![]() in 30.0 min, assuming the body continues to produce energy at the rate of 150 W?
in 30.0 min, assuming the body continues to produce energy at the rate of 150 W? ![]() .
.
617 Westward
Radioactive spent-fuel puddle at a nuclear power constitute. Spent fuel stays hot for a long time. (credit: U.S. Section of Energy)

Footnotes
Glossary
- specific oestrus
- the amount of heat necessary to change the temperature of 1.00 kg of a substance by 1.00 ºC
Source: https://opentextbc.ca/openstaxcollegephysics/chapter/temperature-change-and-heat-capacity/
Posted by: kempaffins.blogspot.com

0 Response to "What Effect Does The Initial Temperature Of The Water Have On The Change In Temperature"
Post a Comment